近日，国际综合性期刊Nature Communications（《自然•通讯》）在线发表了学院在量子人工智能理论方面的最新研究成果。论文题为“Transition Role of Entangled Data in Quantum Machine Learning”（《纠缠数据在量子机器学习中的相变行为》）。学院2021级博士研究生王新彪为论文第一作者，罗勇教授为通讯作者，LETOU.COM乐投为论文第一署名单位和通讯作者单位。

量子纠缠是实现量子计算优势的关键资源。目前，科学家广泛关注如何将量子纠缠整合到量子机器学习模型的各个环节（如纠缠测量和量子演化算子），以期超越传统机器学习模型的性能。相较于同等规模的经典数据，量子纠缠数据因其能够编码更多的信息而备受关注，被认为是实现量子优势的一条有效途径。尽管如此，量子数据的纠缠程度如何具体影响模型性能，仍然是一个尚未解决且颇具挑战性的研究课题。

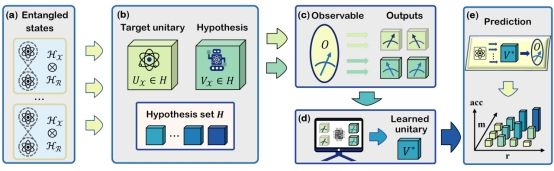
该研究通过建立量子「没有免费午餐」（no-free-lunch, NFL）定理显式地分析了量子数据纠缠程度、测量次数以及训练数据集规模对量子机器学习模型预测误差的影响。现有研究通常认为量子纠缠有助于提升量子机器学习模型的性能，与之不同的是，该研究首次证明量子数据的纠缠程度对预测误差的影响表现出双重效应（即可以是积极，也可以是负面影响），而决定量子纠缠是否提升性能关键在于允许的测量次数。对于足够数量的测量，增加训练数据的纠缠可以有效地减小预测误差，或减少实现相同预测误差所需的训练数据。相反，当允许的测量很少时，使用高度纠缠的数据可能会导致预测误差增大。该研究为设计先进的量子机器学习协议提供了重要指导，特别是对于当前量子计算资源有限的量子计算机而定制的协议。

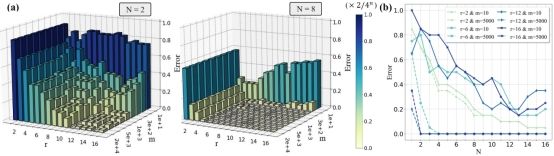
该研究使用了统计学习理论和信息论的相关工具对量子纠缠数据对模型性能的影响进行了精细化的理论分析，并建立了一种对于量子机器学习模型误差下界的分析范式，为研究其他量子计算问题（如量子过程层析、量子误差缓解等）提供一种新的分析方法。

       论文链接：https://www.nature.com/articles/s41467-024-47983-1#Ack1。